제가 원래 도형이나 그래프문제처럼 기하학적인 문제만 연구를해서 수식적인 문제는 잘몰라서

엄두를 못내고있었는데 몇일전에 한번 생각해보기로 했어요. 이글에서는 저의 사고과정을 한번써볼게요!

이문제를 어떻게 만든건지 알아내려면 이 문제가 정확히 어떤 상황인건지

제대로 알아야 하기때문에 일단 한번 풀어봤어요. 해설강의를 통해 수식적인 풀이와 그래프적인 풀이를 모두 봤구요.

이 문제를 풀어보고 든생각이 몇가지 있었는데 일단 굉장히 특이한 문제라는점이었고

또하나는 도저히 이건 인간이 짜맞춰놓은게 아닌거같다는 느낌이었어요. 그래서 이건분명 어떤 "수학적인 자연스러운 과정"

으로 나왔을거라는 생각을 중심으로 연구했어요. 인강해설에서 대부분의 선생님들은 출제자가

이문제를 위해 특별히 함수 f(x)=b*cos(3x)+c*cos(5x) 라는 함수를 짜맞췄다고 하시더라구요. 하지만 저는

출제자가 처음부터 완벽하게 함수 f(x)의 식을 가지고있는 상태에서 문제를 만들었을거라고 생각했어요.

저번에 제가 올렸던 예비평가 18번문제도 f(x)=x*sinx 와같은 함수를 처음부터 가진상태에서 만든거라고 했잖아요?

이문제도 마찬가지일거라고 생각했죠.

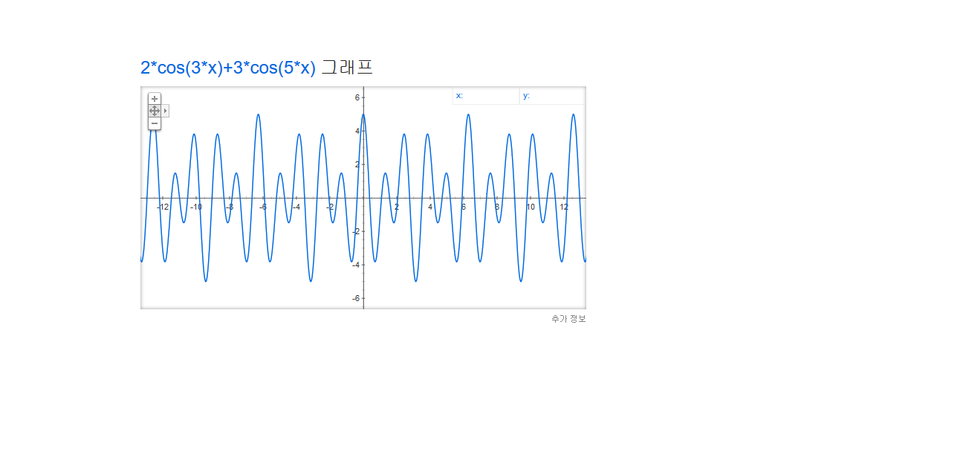
그래서 저는 f(x)를 깔끔하게 2*cos(3x)+3*cos(5x) 라두고 그래프를 봤어요. 

아래 그림처럼 우함수형태의 복잡한 곡선이 나오더라구요. 출제자는 처음부터 이렇게 온전한 함수를 가지고

시작했을거라고 생각했죠.

이 문제를 연구하는데 저를 정말 괴롭게 만들었던 점은 "닫힌 구간 [0,a/2]" 라는 표현과 (나)조건에 나오는 a 가

너무 난해했어요.

수학적인 아이디어가 나오려면 뭔가 분명한 "목표"가있어야하고 "문제상황"이 있어야하고

구하고자하는 이루고하자는 뭔가가 있어야돼요. 그렇지 않으면 아이디어는 나오기 어려워요.

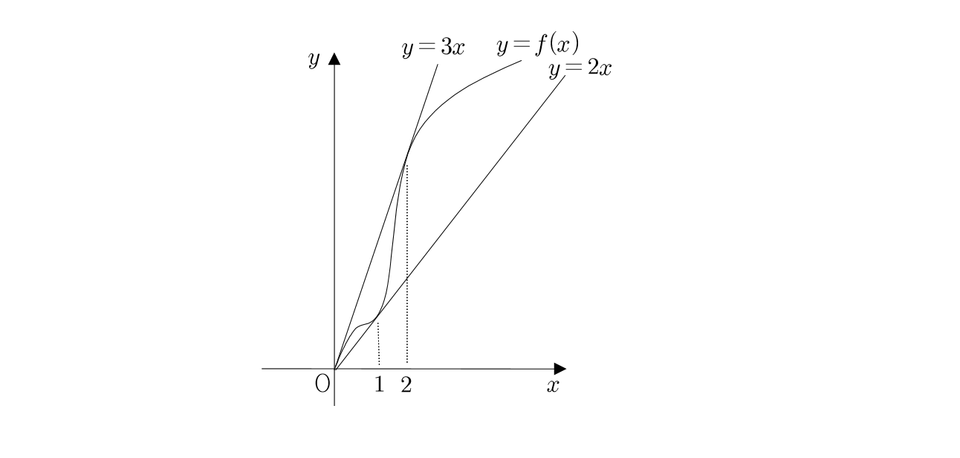
5월 예비평가 18번문제는 f(x)=x*sinx와 같은 함수를 그리는과정에서 아이디어가 나왔으며

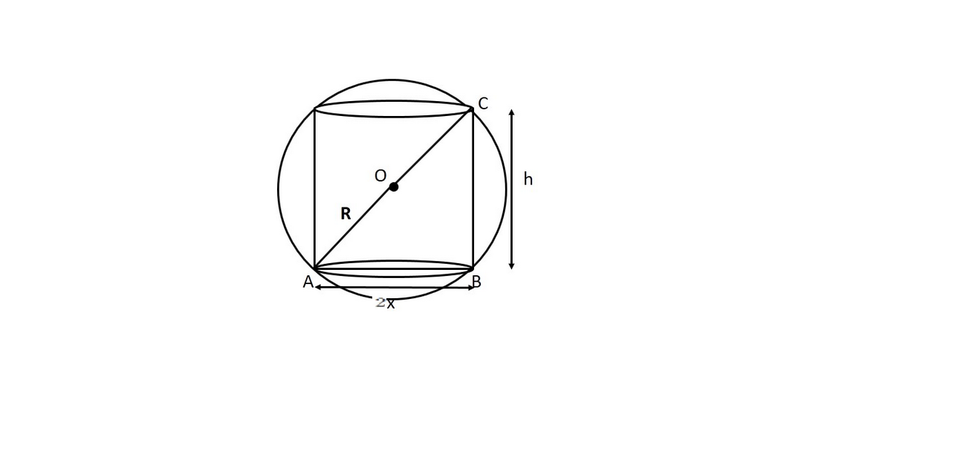
09학년도 수능 25번문제의 아이디어는 구에 내접한 원기둥의 "부피의 최댓값"을 구하는 과정에서

나왔다고 저번에 글을 썼었죠. 함수의 그래프를 그리는것 자체가 일종의 수학적인 문제상황이고

부피의 최댓값을 구하는것도 문제상황이죠. 그래프를 그리기위해 어떻게 그릴지 생각을 하고

노력을 해야 하잖아요? 마찬가지로 부피값을 구하기위해선 문제상황을 분석하고 해결해야돼요.

그러한 과정에서 아이디어가 나오는거죠.

하지만 이문제는 상황이 너무 복잡하고 직관적으로 와닿지가 않아서 대체 어떤 문제를 해결하는과정에서

나온건지를 알수가없었어요. 그런데 이문제의 두가지 특성덕분에 알수있었어요.

 보통 미적분 문제에서는 위의 16수능 30번문제처럼 문제의 초반,중반부분에

함수f(x)의 식이 제시되는데 이 문제에서는 마지막부분에 나오잖아요?  마치 함수f(x)를 찾는것이 궁극적인

목적인것처럼 보이죠.

처음에 생각할때는 b,c의 값이 깔끔한 자연수 일거라 생각을하고 추론을했는데

알고보니 b,c의 값이 복잡한숫자더라고요. 출제자가 굳이 이렇게 복잡한 함수를 가지고 만들리가 없다는 생각이 들었고 

이문제는 처음부터 함수f(x)의 식을 갖고

만든게 아니었다는걸 깨달았어요. 그때부터 이문제는 "f(x)를 구하는 문제상황" 을 해결하는과정에서

만들어졌겠구나 하는 생각이 들었어요.

수학에서 함수f(x)또는 함수y 를 구해야하는 문제상황이 뭐가있을까요?

혹시 미분방정식이라고 들어보셨나요? 대학에서 배우는과목인데요.

방정식하면 대표적으로 x^2-1=0 과 같은게 있죠. 이 방정식의 해라는것은

등식을 만족시키는 x값을 말해요. 따라서 -1과 1이 방정식의 해에요. 미분방정식이라는건

도함수 y',y'' 등이 포함되어있는 방정식인데요. 예를들어서 y+y'=x^2+2x 라는방정식을 생각해봅시다.

이 방정식을 푼다는것은 등식을 성립하도록하는 y를 찾는거에요. y가 어떤함수면, 다시말해

f(x)가 어떤함수면 저 등식이 성립하나요? y=x^2 이면 성립해요. 즉,y=x^2이 이 미분방정식의 해인거죠.

이거말고도 밑의 7가지 미분방정식처럼 아주 복잡한 미분방정식이 많고 정말 풀기어려운 미분방정식이 많아요.

어쨋든 저 등식을 만족하도록하는 y를 찾기만하면되는데 쉽지않아요.

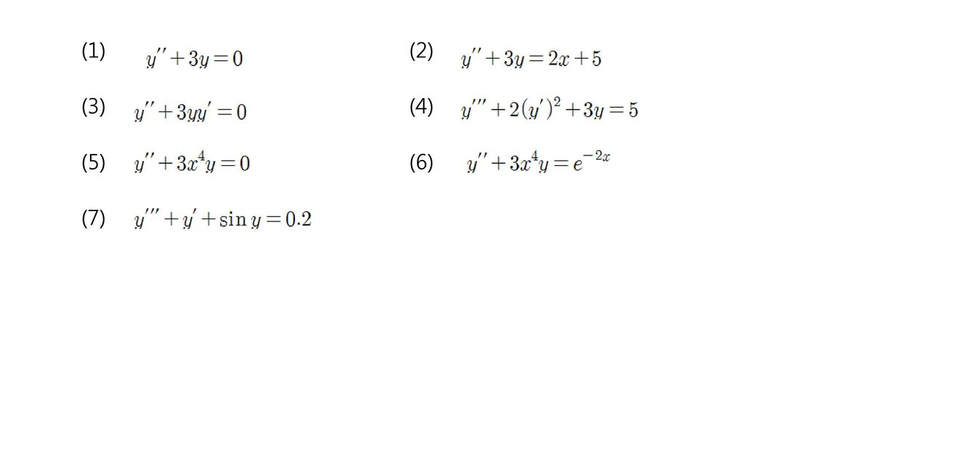
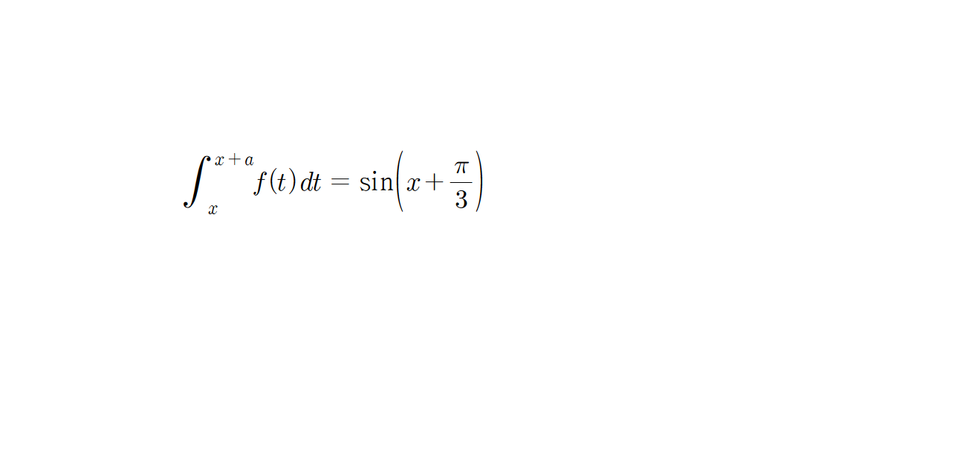
출제자가 처음부터 함수f(x)를 가진상태에서 문제를 만든게 아닌거같다는 느낌을받았을때

혹시 이 등식을 만족하는 함수f 를 찾는과정에서 이문제의 아이디어가 나온게 아닌가 생각했어요.

그리고 미분방정식은 미분이 포함된 방정식이니까, 혹시 위의식처럼 적분으로 이루어진건

적분방정식이 아닐까? 생각을했고 실제로 적분방정식이란게 존재하는지 구글에 쳐봤는데 실제로 있더라고요.

그리고 적분방정식은 학부때 배우지않고 대학원과정이라고 하더라고요.

적분 방정식

적분 방정식(積分方程式)은 수학에서 미지의 함수에 대한 적분 연산을 포함하는 방정식을 말한다. 미분 방정식과 관계가 깊으며, 어떤 문제들은 미분방정식, 적분방정식 모두로 나타낼 수도 있다.

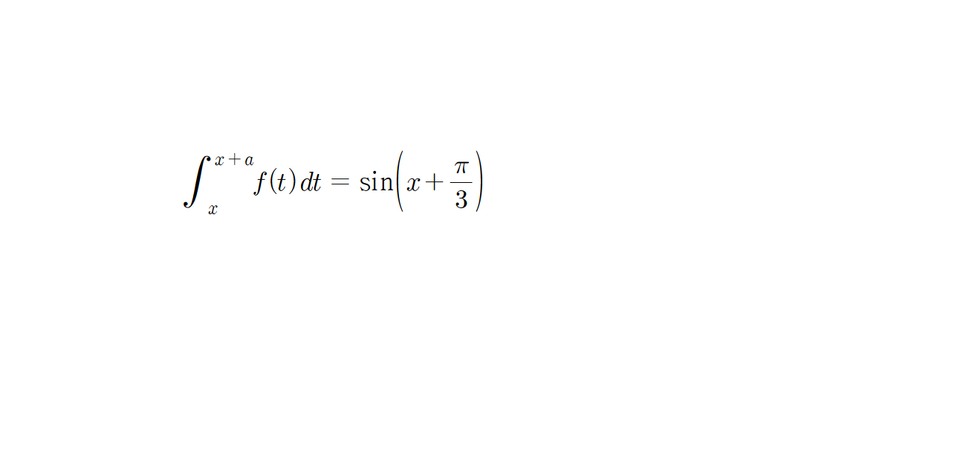
이 적분방정식을 푼다는건 아까와 마찬가지로 이 등식을 성립하도록하는

f(x)를 찾는거겠죠? 그런데 해가있다는 확신이 있는상태에서 적분방정식을 풀어야 할거잖아요?

해가없는데 풀면 헛수고니까요. 그래서 오른쪽의 함수도 아무 함수나 올수있는게 아니라 저런형태의 적분방정식이

해를 갖도록하는 함수가 올거에요 (이걸 판정하는방법은 대학원과정 일거같네요)

그래서 오른쪽에 sin(x+π/3)함수가 온거죠. 그렇다면 왜 구간에따라서 f(x)가 다르게 나오는걸까요?

원래 x^-1=0 과같은 일반적인 방정식에서는 x=-1or1처럼 해가 깔끔하게 나오지만 적분방정식은

특성상 구간에따라 해가 달라지는 성질이 있는거같아요. 물론 모든 적분방정식이 다 그런건 아니겠죠.

아무래도 일반적인 방정식처럼 "숫자"가 해가아니라 "함수"가 해이다보니 그런 성질이있는게 아닌가 싶네요.

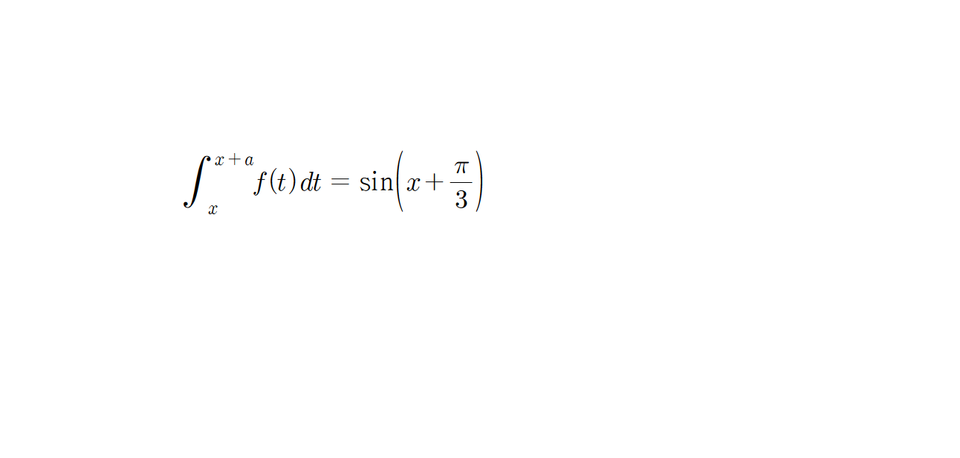
그래서 출제교수님(or수학자)이 이런 적분방정식을 풀어보니까 일단 구간 [-a/2,a/2] 에서

해가 f(x)=b*cos(3x)+c*cos(5x) 로 나온거에요.

이제 a/2 오른쪽 부분에서의 해를 구하면 돼요.

f(x+a)=f(x)+cos(x+ π/3)이니까

구간 [a/2,3a/2]에서의 함수f(x)의 식은  b*cos(3x)+c*cos(5x) 와 cos(x+ π/3)를 a만큼 평행이동 시킨다음에

더하면 되니까 구간 [a/2,3a/2]에서

f(x)=cos(x-a+ π/3)+ b*cos(3(x-a))+c*cos(5(x-a)) 가

적분방정식의 해가되네요. 이와같은 원리로 다른구간도 해를 구했을거에요.

b*cos(3x)+c*cos(5x)도 우함수고 cos(x-a+ π/3)+ b*cos(3(x-a))+c*cos(5(x-a))도 우함수니까

아무리 평행이동시켜서 더해도 결국 우함수잖아요?

그러면 함수 f(x)가 우함수라는사실을 알게되고 f(x)=f(-x) 라는걸 알게돼요.

이 조건들을 쓰면 a,b,c의 값들을 구할수있고 이 적분방정식의 해가 완전히 구해지는거죠.

이처럼 수학자들도 이 문제를 푸는수험생과 마찬가지로 저 a,b,c를 구하는

과정을 거쳤을 거에요. 수식적으로 우함수적분의 대칭성을 이용해서 푼사람도 있을거고 그래프적으로

구한사람도 있겠죠.

즉,이 적분방정식의 전반적인해가 f(x)=b*cos(3x)+c*cos(5x)라는걸 구하는과정은 대학원 이상의 과정인것이

고 마지막에 상수 a,b,c를 구하는과정은 고등학교과정으로도 충분히 해결할수있는거죠. 그래서 이걸 출제한거같아요

쉽게말해 적분방정식 풀이의 엔딩으로 이문제를 만든거고 이 문제의 상황자체가 적분방정식풀이의 한복판인 셈이죠.

적분방정식을 대학원에서 다루는거보면 저함수 f(x)를  통째로 구하는 과정은 매우 복잡하고 어렵겠죠?

혹시 평가원이 적분방정식으로 만든문제가 더 있나 궁금해서 한번 찾아봤어요. 대표적으로 떠오르는문제가

아래문제였어요.

2013학년도 수능 12번문제에요. 이 문제에 나온 등식을 살펴보면 인테그랄이 들어있잖아요?

즉, 적분방정식이라는 얘기고 이 적분방정식을 만족하는 해를 구하기위해서는 0부터 1까지 xf(x)의 적분값을 알아야하는거죠.

저값을 구하면 이 적분방정식의 해는 f(x)=e^(x^2)+ e-1 이 돼죠.

이 문제도 (나)조건을 보면 적분방정식이 나와있네요. 이 적분방정식의 해를 구하면

x≤b 구간에서는 y=a(x-b)^2 + c 가 해가되고 x≥b 에서는 y=c 가 해가되는거죠.

이문제도 17학년도 6평 30번처럼 구간에따라 해가 다르게 나오는 문제네요.

2014학년도 9월 30번인데 이문제도 문제에 나와있는 적분방정식의 해 g(x)함수를 구하면

구간에따라 해가 다르게나와요. 이문제는 적분방정식이 두개있는거같은데 혹시

연립적분방정식이 아닌가? 싶네요

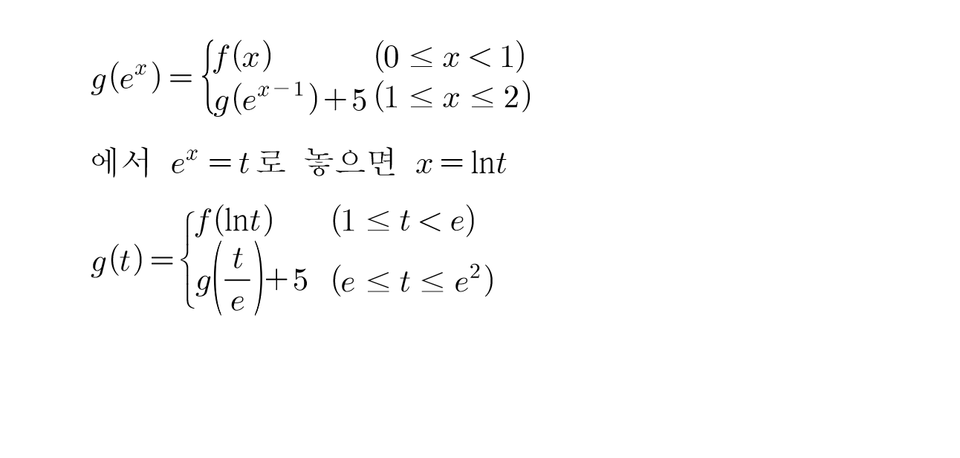
12수능 28번 문제에요. 이문제도 F(g(x))=F(x)/2를 적분식으로 바꾸면 적분방정식이 되네요.

이문제에 나오진않았지만 g(x)가 뭔가 존재하겠죠? g(x)는 아마 3차함수의 역함수일건데요.

적분방정식의 해를 구해보면 f(x)=3(x-1)^2+5 가 돼요. 이문제는 순서를 거꾸로해서 만들었네요.

해가 이차함수처럼 대칭성을 지닌 함수가 나와야 이문제처럼 대칭성을 이용한 아이디어가 가능할거같군요

5월 예비평가 21번 문제에요.

이 문제는 ㄷ보기에 적분방정식이 있네요. 저 적분방정식의 해를 구하면 문제에서 주어진함수가

나오게 되는거죠. 이 함수의 여러가지 성질들이 있을거잖아요? 그 성질들중에서 ㄷ과 관련있는 성질을 

ㄱ,ㄴ에서 물어보는거 같아요.

ㄷ을 가지고 문제를 만들었을거니까 ㄷ은 참인걸로 만들었을거같다고 생각했는데 답지보니까 ㄷ이 참이더라고요.

(다)-> 적분방정식

(가),(나) ->q/p를 구하기 위해 필요한 적분방정식의 해 f(x)의 성질

그동안 행령진위 문제를 풀면서 사람이 짜맞췄다고 하기에는 믿을수없을정도로 너무

정교하게 설계가되있어서 어떻게 만드는건지 알수가없었는데 혹시 예비평가 21번문제와

비슷한 원리가 아닐지 생각되네요. 이건 더 생각을 해봐야겠네요.

이 문제는 생각중인 문제인데 적분방정식이 안나와있어서 다른방식으로 생각해봐야할거같아요.

읽어주셔서 감사합니다!

ps. 이게 100프로 맞는건지는 잘모르겠어요 ㅠ 참고삼아서 봐주세요!